[Up: Mathematical representations]
[Previous: Matrix applications]
[Next:]
 Bikexprt.com Web Site
Bikexprt.com Web Site
| [Top: John S. Allen's Home Page] [Up: Mathematical representations] [Previous: Matrix applications] [Next:] |
|
Matrix tunings and the permutation lattice
John S. Allen
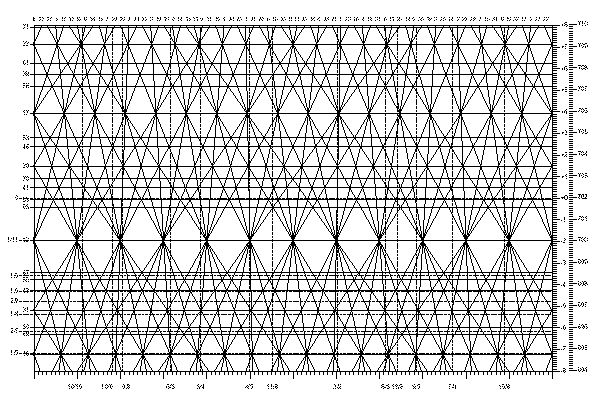
The permutation lattice graph | Horizontal axis: frequency | Vertical axis: tempering |
Equal temperaments | Open
temperaments | Using error bars
The previous article showed how a musical tuning can be described as a two-dimensional matrix, and gave several examples showing how this description corresponds to the structure of practical musical tunings and instruments. We now take a decisive turn in a new direction, examining tunings which can only be described mathematically as a two-dimensional matrix. We alter our matrix tuning formula to 2nFx = 2(n - q) xpFR, or Fx,n = 2(n - q) xpFR where x is a real number between 1 and 2, and p is an integer. Except for just intonation, all of the tunings described in previous articles had equal steps. With this new formula, the steps in each dimension of the matrix are equal, but when placed in order of frequency, steps need no longer be equal. One dimension of the matrix represents octaves as 2n; the other dimension represents the powers of x. Unlike the term m/k used in our earlier formulas, x need not be commensurable with the octave, since x is no longer burdened with defining the octave. The 2-dimensional matrix of musical pitches now reveals three major advantages: 1) The second dimension allows for more freedom in setting pitches, a freedom which has been widely used in historic and experimental tunings; 2) The tuning matrix maps to a 2-dimensional keyboard matrix, allowing a much larger number of keys and of musical pitches in each octave 3) The arrangement of keys in such a matrix is self-consistent, resulting in ease of playing. The large graph accompanying this article is a compact and comprehensive representation of the structure of 2-dimensional matrix temperaments. If you have trouble understanding the graph, the sections on musical scales and intervals in Sir James Jeans’s book Science and Music and Hermann von Helmholtz’s On the Sensations of Tone provide a good introduction. Here is a small version of the graph. You may also view a resizeable version in Adobe Acrobat format so you can zoom in and out, or print it. Thanks to Bart Pauwels for producing a computer-generated version of this graph. It is much cleaner and clearer than my own hand-drawn version which I had posted earlier. |
(resizeable version of
graph, PDF document)
The resizeable version will open in a new window. Leave it open
so you can refer to it while continuing to read this page.
| The graph is an example of what mathematicians call a permutation lattice. It
shows how the powers of a number change when that number is decreased or increased
slightly. In the present permutation lattice, we vary the frequency ratio of the musical
fifth slightly to generate musical temperaments --including the familiar 12-tone equal
temperament and an infinite number of others. This graph shows musical temperaments in
which the interval of the perfect fifth is within ± 8 musical cents relative to the just, 3/2 ratio. The horizontal axis: frequency Common musical temperaments are based on the frequency ratio of the octave, 2/1, and of the musical fifth, nominally 3/2. All frequencies in a temperament are reached through octaves in combination with series of fifths. Here's an example: G stands a musical fifth above C, at the frequency ratio of 3/2. The square (second power) of the 3/2 ratio is 9/4, the D in the next higher octave. Other frequencies are reached in the same way. Adopting the musical convention that assigns musical pitches with fundamental frequency ratios of 2/1 (octaves) to the same pitch class with the same letter name, we may transpose them up or down by one or more octaves. Mathematically speaking, we may multiply or divide any of the frequency ratios by 2 or a power of 2 to keep them within the range between 1 and 2. This is the same approach as in the previous article’s discussion of how equal temperament may be derived using musical fourths and fifths. The horizontal axis of the permutation lattice represents a frequency range covering a ratio of 1 to 2, a musical octave. The horizontal scale of the graph is logarithmic, so equal frequency ratios are represented by equal horizontal distances anywhere on the diagram. Here's the small version again with these features labeled: |
|
<<--- One octave (2/1 ratio), logarithmic scale --->> |
Several specific frequency ratios are indicated in the graph by dashed vertical lines
and by the fractions at the bottom of the graph. These frequency ratios include some used
in diatonic musical scales in just intonation:
Also included in the graph are exotic frequency ratios based on harmonic partials up to the 13th:
The vertical ruler next to the right side of the graph corresponds to the detuning, or tempering, of the musical fifth over a range of -8 to +8 musical cents (hundredths of a musical semitone) above and below the frequency ratio 3/2. The ruler shows both the deviation in cents from the 3/2 ratio and the number of cents relative to the 1/1 ratio. On the scale, you can see that the 3/2 ratio corresponds to approximately 701.95 musical cents and the fifth in equal temperament corresponds to 700 musical cents, slightly less than a 3/2 ratio. The values for musical fifths in other temperaments are found at other heights in the graph. A little to the right of the middle of the graph, you will see a dashed, vertical line representing the just fifth (3/2). Assuming that the graph represents an octave from C to C, the fifth is a G. Crossing the dashed, vertical line is a solid line which is almost but not quite vertical. Rather, it is slanted slightly to the right at the top and to the left at the bottom. The slanting of the line corresponds to the tempering of the musical fifth, to slightly more than the just ratio of 3/2 at the top and slightly less at the bottom. In our formula Fx,n = 2(n - q) xpFR, the tempering corresponds to slight alterations in the value of x. As already stated, we reach each frequency in our sequence of musical fifths by multiplying or dividing the previous frequency by 3/2, and transposing it up or down an octave if necessary. D, the major ninth, is at 3/2 ratio to the G, and a 9/4, or (3/2)2 ratio to our original C. Since 9/4 would be off the chart to the right, we divide it by 2 to bring it down by a musical octave to the major second, 9/8. In our formula Fx,n = 2(n - q) xpFR, the progression from C to G to D is represented by our setting the value of p to 0, 1 and 2 respectively, and the octave transposition is achieved by adjusting the integer value of q so that 1 <= Fx,n /FR < 2. |
|
A little to the right of center ^, the 3/2 dashed line |
9/8 line rises from the second fraction from left, above |
| Now look at the 9/8 dashed line, which is the second vertical dashed line from the
left side of the graph (in a pair of dashed lines which are close together). Since the
nominal 9/8 ratio accumulates the tempering of two 3/2 ratios in sequence, the tempered
approximation of the 9/8 frequency varies by ±16 musical cents, twice as much as our
original tempered approximation to 3/2. In the graph, the most nearly vertical solid line
near the 9/8 line slants to the right twice as much as the solid line which crosses the
3/2 dashed line. As we continue the sequence of upward fifths, the solid line representing each new ratio slants by an amount representing an additional ±8 cents. We therefore generate a series of lines which tilt father and farther away from the vertical, representing frequencies which correspond to higher powers of x. The graph shows 35 such lines. In the same way, we also draw lines representing negative integer values of p and descending series of fifths from C, to F, Bb, Eb and onwards. These lines tilt to the left at the top and to the right at the bottom. The graph also shows 35 of these. All in all, the diagram shows 71 steps through fifths, with 35 fifths upward and 35 downward from the central C. Since the slopes of the lines in the graph representing the tempered intervals are different, the lines cross. Just below the center of the graph, the lines cross at 13 points representing the 12 frequencies of the 12-tone equal temperament (The 13th point is the octave, at the right side of the graph.) |
|
12- |
| There are only 12 frequencies in this temperament because the series of musical fifths
(with octave transpositions) repeats after 12 fifths. The numbers at the top of the chart
represent the number of fifths from the starting frequency to the musical fifth
represented by the closest angled line. The lines in each bundle have numbers which differ by multiples of 12. So, for the half-bundle at the left of the chart, the rightmost lines are musical fifths +24 (in the sequence beginning C-G-D-A...) and -24 (in the sequence beginning C-F-Bb-Eb...); the intermediate lines are musical fifths +12 and -12; and the vertical line is the central interval of the sequence, musical fifth 0. The numeric indications for other bundles work in the same way. In a closed, equal temperament, the series of fifths closes on itself to form a circle of fifths, within the number of fifths available to the player. A practical example is the twelve-tone equal temperament including both the white and black keys of the traditional keyboard. In a closed series of fifths, the same pitch may be reached by different musical routes, stepping in either direction through the series of fifths: for example in the 12-tone equal temperament, F# is reached by going upward through fifths from C, and Gb is reached by going downward through fifths from C in the conventional 12-tone temperament. Besides the 12-tone crossings, there are numerous other crossings at other levels in the graph. These other levels represent other equal temperaments which, like the 12-tone temperament, are indicated by horizontal lines across the graph. Numbers at the left side of the graph give the number of tones in each equal temperament. These temperaments will be discussed in more detail in the next article in this series. Horizontal levels in between the horizontal lines of the graph correspond to temperaments in which all musical fifths are equal, but in which no number of fifths up to 71 corresponds to a whole number of musical octaves. These are open temperaments. To state this another way, the series of fifths does not close on itself to form a circle of fifths, at least not within the number of fifths shown in the graph. Some practical examples of open temperaments are the Pythagorean scale of just fifths, the diatonic modes playable on the white keys of the traditional keyboard without using the black keys, and the pentatonic sacles playable on the black keys. The historic 1/4 comma mean-tone temperament is another example of an open temperament. In order to place the major thirds exactly in tune, the fifths in the mean-tone temperament are somewhat flatter than in 12-tone equal temperament. Because of its flatter fifths, the mean-tone temperament does not close after 12 fifths. On a conventional musical keyboard, all of the musical fifths in the mean-tone temperament are the same except for one, the so-called "wolf fifth." Within the range of musical key signatures in which the wolf fifth (and related wolf thirds and sixths) can be avoided, the mean-tone temperament sounds more harmonious than 12-tone equal temperament. But with only 12 keys per octave on a conventional musical keyboard, modulation beyond two or three sharps and flats is not possible in the mean-tone temperament without bringing out the howling wolves. The general keyboard described in another article on this site avoids the wolf problem by continuing the series of fourths and fifths beyond 12. This keyboard has several dozen keys per octave, in an array based on the sequence of musical fourths and fifths. Using error bars to evaluate temperaments The purpose in preparing the graph with this article was to examine which temperaments would be most suitable for the general keyboard. By laying a horizontal ruler across the graph, it is possible to find the temperaments, both open and closed, which play well in tune on the general keyboard. Now let's see how we can find out how accurately temperaments approximate just intonation. We use an overlay for the permutation lattice which shows error bars indicating the difference between just intervals and tempered ones. The slanted lines of the permutation lattice graph are visible through the overlay. Here is a small version of the error bar graph. A large version of the error bar graph. is available as a PDF document. (Thanks again to Bart Pauwels for generating an improved version of this graph). |
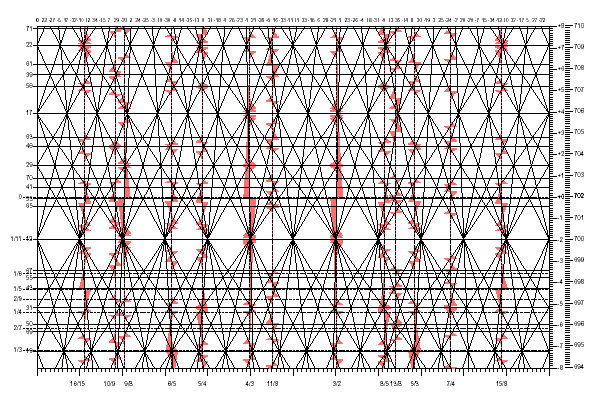
(large version of error bar graph)
A wide error bar indicates that a tempered frequency and a just frequency are close to
one another, and a narrow error bar indicates that these frequencies are farther apart.
Mathematically speaking, each error bar is scaled approximately as the inverse of
the difference between the tempered frequency (slanted line in the permutation lattice)
and the just frequency (vertical, dashed line) which it 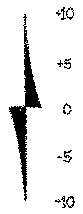 approximates. As the tempered frequency
rises toward the just frequency, the error bar widens on the left side of the vertical
line representing the just frequency. Where the just and tempered intervals are equal, the
error bar jumps across to the right side. The error bar then becomes narrower as the
tempered frequency increases away from the just frequency. The total range covered by an
error bar is ±10 musical cents, as shown at the right. approximates. As the tempered frequency
rises toward the just frequency, the error bar widens on the left side of the vertical
line representing the just frequency. Where the just and tempered intervals are equal, the
error bar jumps across to the right side. The error bar then becomes narrower as the
tempered frequency increases away from the just frequency. The total range covered by an
error bar is ±10 musical cents, as shown at the right.At horizontal levels in the graph representing equal temperaments, slanted lines cross and several error bars lie on top of one another. Musical fifths near the center of the series of 71 are of more interest, because these fifths are accessible on smaller keyboards and/or with less hand motion. No error bar is completely hidden, since the ones representing the more remote fifths (more steeply slanted lines) change more abruptly and peek out from behind the others. The number of the musical fifth which corresponds to each error bar is indicated next to that error bar. By placing a straightedge horizontally across the overlay graph and examining the error bars, we can see which temperaments offer good approximations to the just intervals. Those temperaments, both open and closed, are indicated at the left side of the overlay graph. The following article will discuss what the error bar graph reveals about specific temperaments. |
| [Top: John S. Allen's Home Page] [Up: Mathematical representations] [Previous: Matrix applications] [Next:] |
Contents © 1997 John S. Allen Last revised 6 May 2003 |